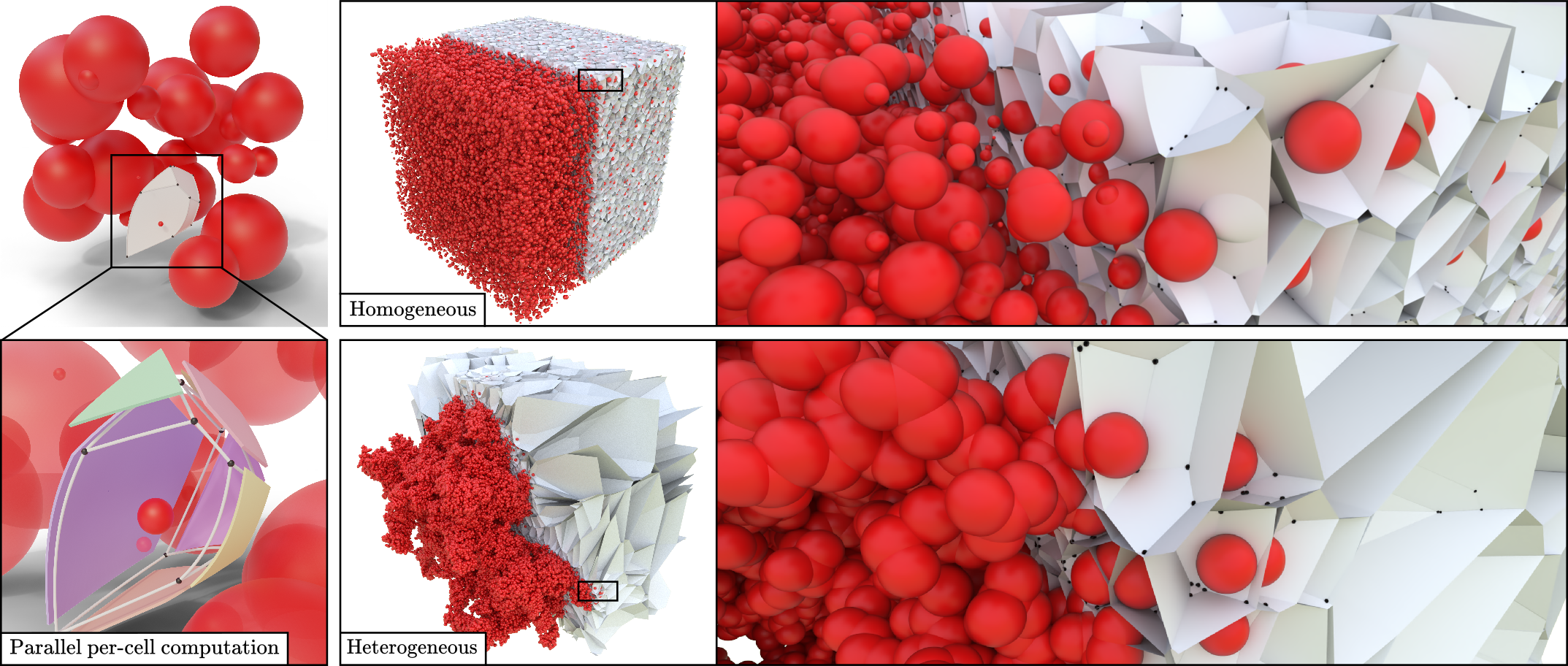
We present a novel comprehensive construction algorithm of Apollonius diagrams designed for GPUs. Efficient and robust algorithms have been proposed for the computation of Voronoi diagrams or Power diagrams. In contrast, Apollonius cells are neither convex nor bounded by straight boundaries, making their computation complex, especially in more than two dimensions. Their parallel computation also represents a challenge because of the sequential nature of state-of-the-art algorithms. In this article, we tackle the computation of these diagrams from the geometry of their cells. Our strategy is based on a core cell topology update allowing the iterative insertion of new sites found through nearest neighbor queries. To benefit from the highly parallel environment of modern GPUs and fit their memory restriction, we define a lightweight data structure allowing the representation of the complex topology of Apollonius cells. Additionally, we provide several space exploration procedures for their efficient construction under both homogeneous and heterogeneous spatial distributions. Our method outperforms the fastest state-of-the-art CPU implementation while computing the complete geometry. As a possible use case, we show an application for molecular illustration.
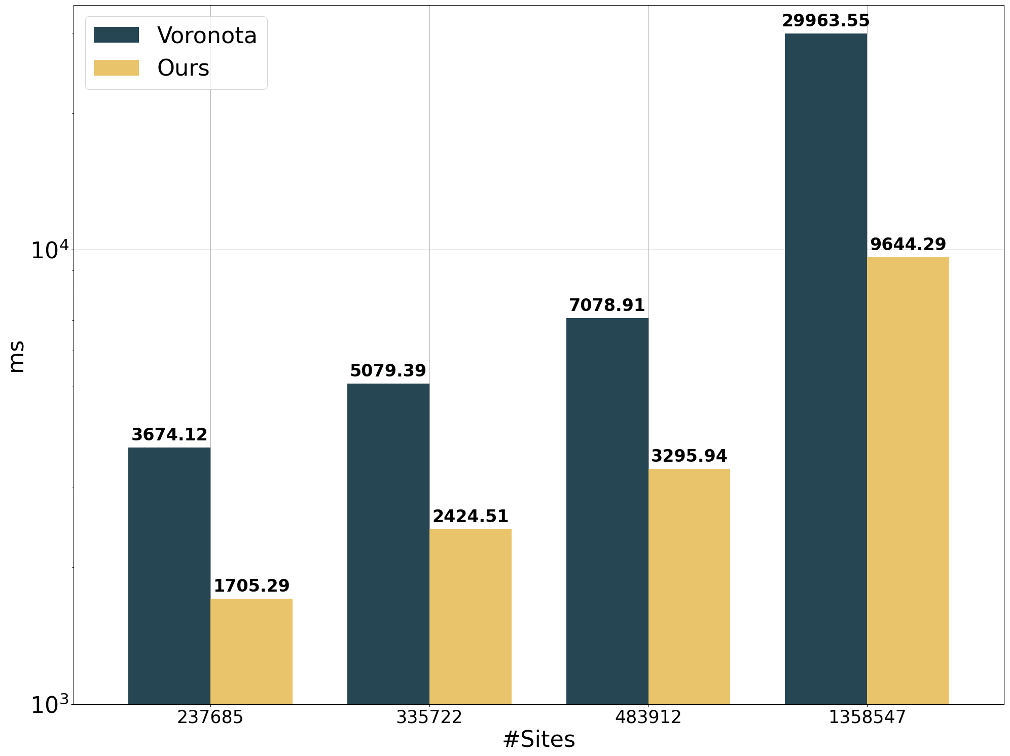
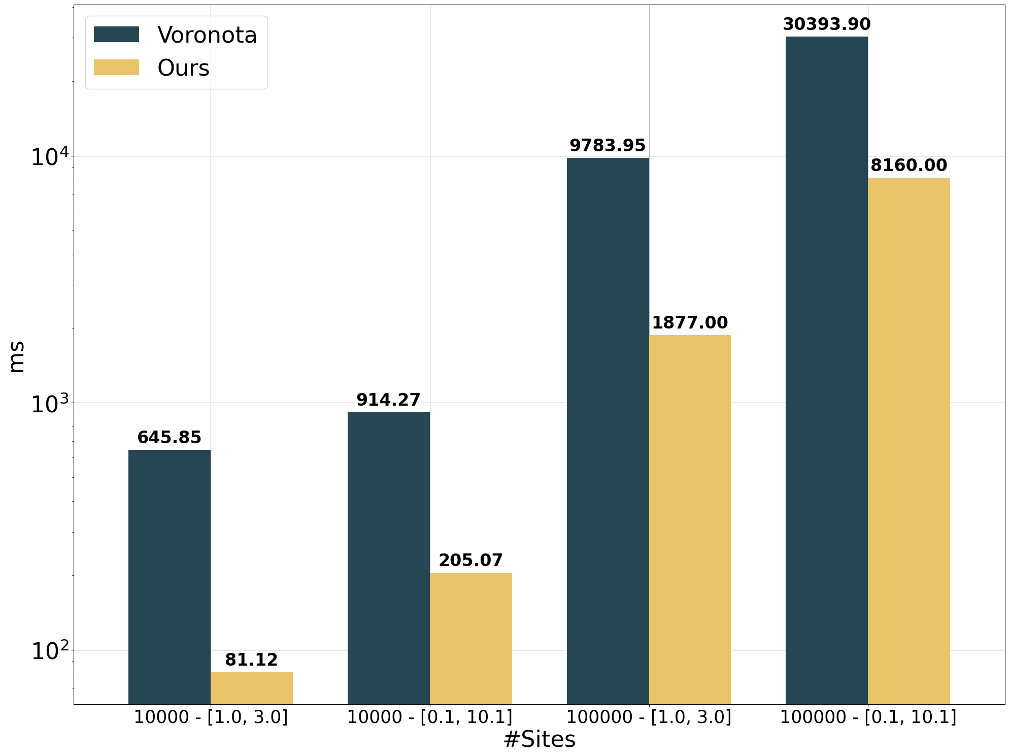
We compare the performances of our method to Voronota, a library targeting fast computation of Apollonius diagrams vertices.
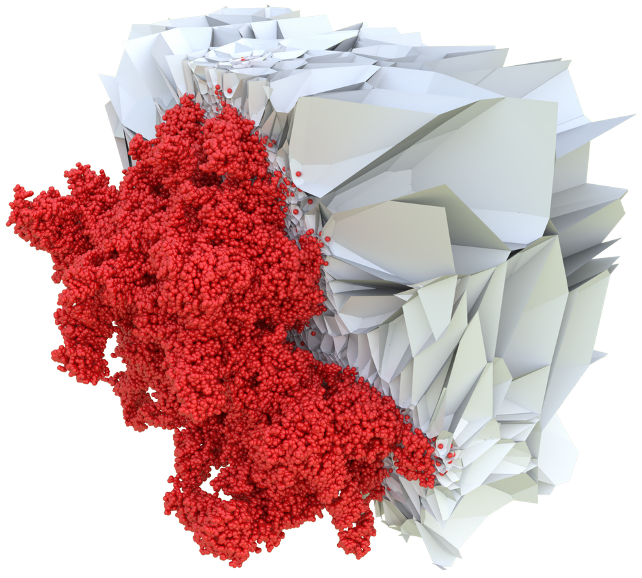

Based on our method, we developped an application filtering interesting protein cavities based on the visibility and the size of Apollonius vertices.
This can be used for protein structural analysis but also for illustrative rendering (as proposed by Lindow et al.).

@article{PlateauHolleville2025,
author = {Plateau--Holleville, C. and Stamm, B. and Nivoliers, V. and Maria, M. and Mérillou, S.},
journal = {ACM Transactions on Graphics},
title = {In Search of Empty Spheres: 3D Apollonius Diagrams on GPU},
year = {2025},
volume = {44},
number = {4},
pages = {1--15}
}